Ahrim Han, Ph.D.

Ahrim Han, Ph.D.

Fast refactoring candidate assessment metric

Period: March 2011 - December 2014

Table of Contents

  1. Motivation and Goal
  2. Method
    2.1. Assessment in the refactoring identification process
    2.2. Software design is captured into a graph
    2.3. Delta Table calculation
  3. Evaluation
    3.1 Research questions
    3.2 Data sets
    3.3 Comparators
    3.4 Evaluation measures
  4. Results
    4.1 Efficiency
    4.2 Usefulness
  5. Conclusion
  6. Papers
  7. Awards

Motivation and Goal

The cost for assessing refactoring candidates is computation-intensive. For automating refactoring identification, previous studies have limitations for assessing the impact of a large number of refactoring candidates.

In this project, I propose a fast refactoring candidate assessment metric, Delta Table. This metric is an efficient method for assessing the impact of refactoring candidates on maintainability based on matrix computation, which is approximate but fast. This metric helps to select the most efficient refactoring candidates for the large-scale software.

Method

Assessment in the refactoring identification process

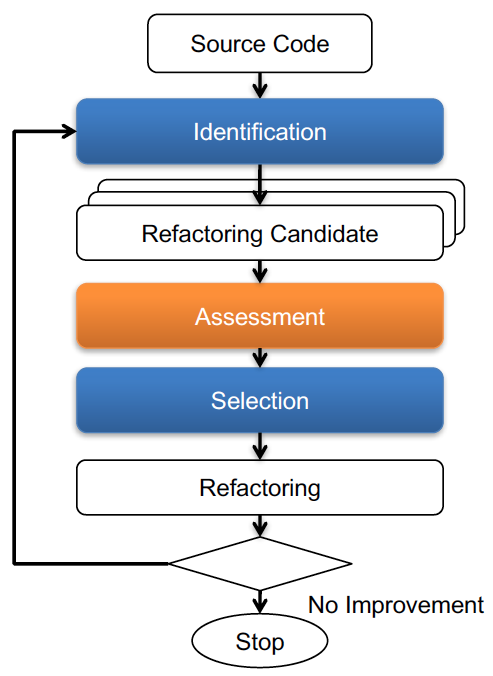
researchDeltaOverview
To identify refactoring sequence automatically, the possible moves of methods to classes in the system (i.e., refactoring candidates of Move Method) are assessed the using the Delta Table and the most improving refactoring is selected and applied. This process is iterated until there are no more improvements.

Software design is captured into a graph

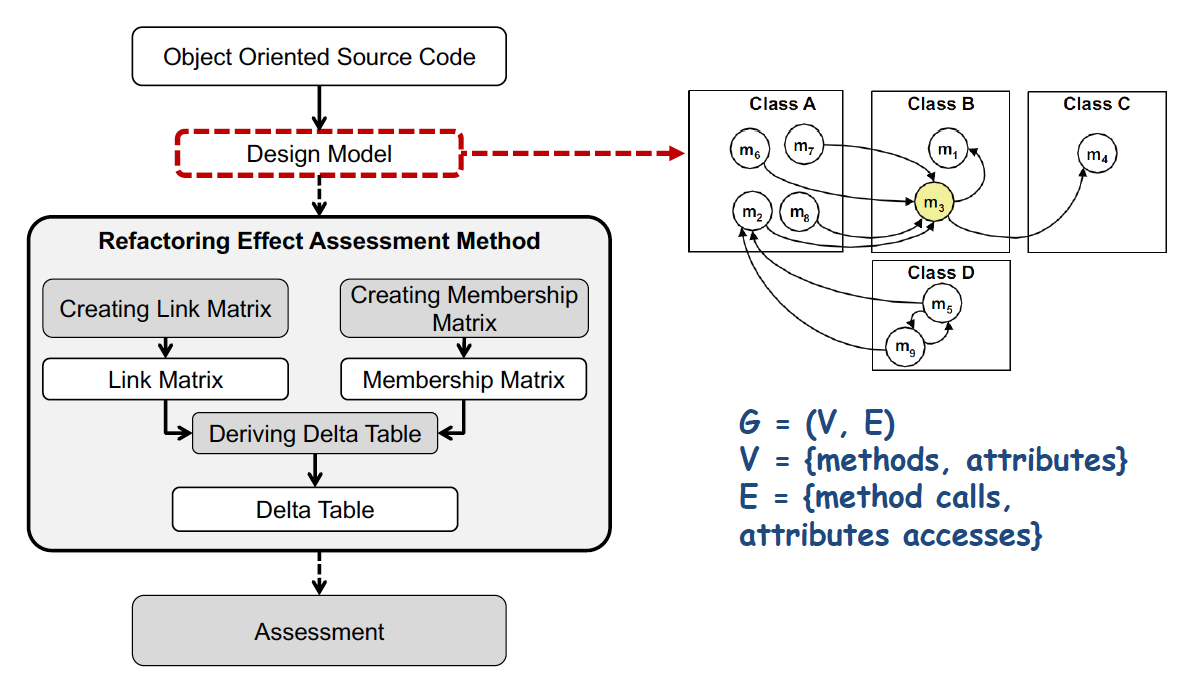
researchDeltadesign
From the object-oriented source codes, the software design is captured into a graph. The entities of methods and attributes are mapped into vertices (V) and their relations such as method calls and attribute accesses are mapped into edges (E).

Delta Table calculation

The Delta Table (D) is the matrix (rows: entities, columns: classes). Each element in the Delta Table (D_{ij}) represents the variance of the number of external relations (i.e., relations across the classes) when moving entity i to class j.

Illustrative calculation of Delta Table
researchDeltaCalculation

Step of the Delta Table calculation
From the design graph, the link and membership matrices are constructed.

  • Link matrix (L)
    • L(e1, e2): entity e1 has a relation to entity e2
    • Lint | Lext:
      internal | external relations that are associated between entities in the same class | across the classes
  • Membership matrix (M)
    • M(e, C): entity e is placed in class C

The projection matrix is produced by multiplying the link and membership matrices.

  • Project matrix (P)
    • P(e1, C): entity e1 has a relation to an entity placing in class C
    • Pint | Pext:
      internal | external project matrix
      • Pint = Lint x M, Pext = Lext x M

The formulation is devised by taking the effects (simulating) of moving entities.

  • inverse function() is applied to the internal project matrix because moving an entity to other classes will potentially increase the external relations in the system. Inverse internal project matrix (invPint) represents the effects of increased external relations when moving entities that have had internal relations. For example, let an entity ei has a relation with another entity within the same class C1. When ei moves to other class C2, then the existing internal relation switched to the external relation: invPint(ei, C1) = 0 (no effect) and invPint(ei, C2) = 1.

  • inverse function()

  int [][] invPint = new int [num_entities][num_classes]; //inverse internal project matrix

  for (e = 0; e < num_entities; e++)
  {
    for (c = 0; c < num_classes; c++)
    {
      if (Pint[e][c] != 0) //an entity `e` has a relation with another entity within the same class `c`
      {
        for (i = 0; i < c; i++)
        {
          if (i != c)
            invPint[e][i] = Pint[e][c];
            //moving entity `e` to other classes increases
            //the external relation(s)
          else
            invPint[e][c] = 0; //remaining in the same class `c` has no effect
        }
      }
        invPint[e][c] = 0;
    }
  }

  return invPint;
  • Similarly, minus is applied to the external project matrix because moving an entity to the classes that have had external relations will decrease the external relations in the system.

The final formulation of the Delta Table (D) is:

D = invPint - Pext

Evaluation

Research questions

RQ1. Efficiency: By how much our method is efficient for assessing the impact of refactoring candidates?
RQ2. Usefulness: Does the refactoring identification approach based on our method help improve maintainability?

Data sets

Open source projects written in Java

Name (Version)jEdit (jEdit-4.3)Columba (Columba-1.4)
TypeText editorEmail clients
Class #9521506
Methods #64878745
Attributes #35233967

Comparators

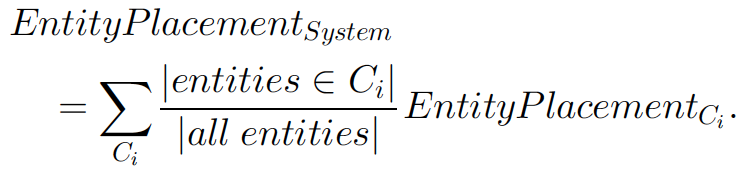
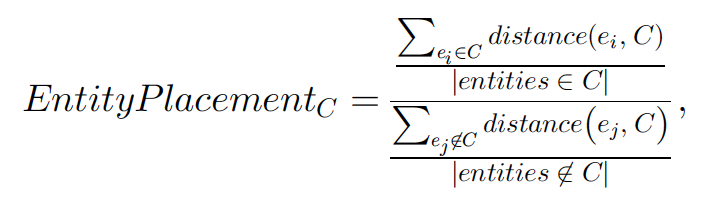
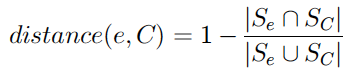
Evaluation measures

Evaluation measures
- Total time
- Maintainability metric: MPC (Message Passing Coupling)

For maintainability metric, MPC (Message Passing Coupling) is used. MPC is a widely used coupling metric for measuring maintainability of software design. The lower coupling means the more maintainable software.

Results

1. Efficiency: By how much our method is efficient for assessing the impact of refactoring candidates?

  • The total time required to perform the refactoring identification approach with the Delta Table is much less than the approach with the EPM.
  • Maximum time per iteration in our approach is the time for the first iteration.
  • As system become larger, computation time is increased.
  • Rate of increased time with respect to the system size is much less in our approach.
  • Total time (sec)
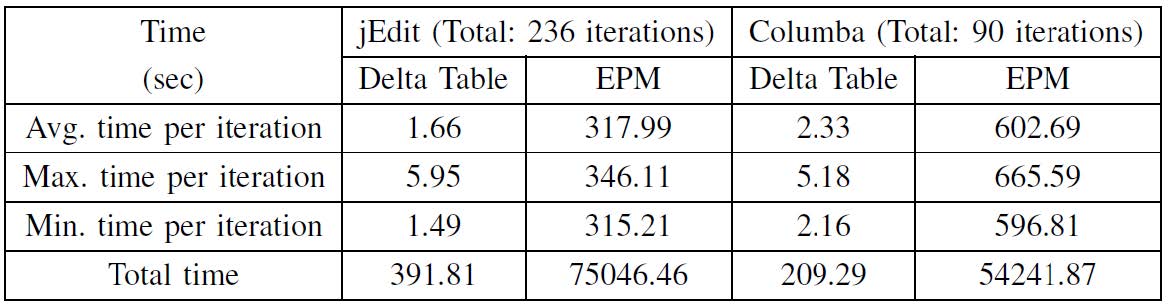
    graphCK
    • The total time required to perform the approach with the Delta Table is much less than the approach with the EPM.
    • Maximum time per iteration: time for performing the first iteration including constructing the design graph, calculating the link and membership matrices (e.g., jEdit: max. 5.95 [sec] > avg. 1.66 [sec], Columba: max. 5.18 [sec] > avg. 2.33 [sec])
    • As system become larger (jEdit: 952 classes, Columba: 1506 classes), computation time is increased.
    • Rate of increased time with respect to the system size is much less in our approach (e.g., jEdit at 90 iterations, our approach: 154.63[sec], approach with EPM: 28,622[sec])

2. Usefulness: Does the refactoring identification approach based on our method help improve maintainability?

The values of maintainability metric for our approach are increased in both projects (jEdit and Columba).

  • Maintainability metric for jEdit jEdit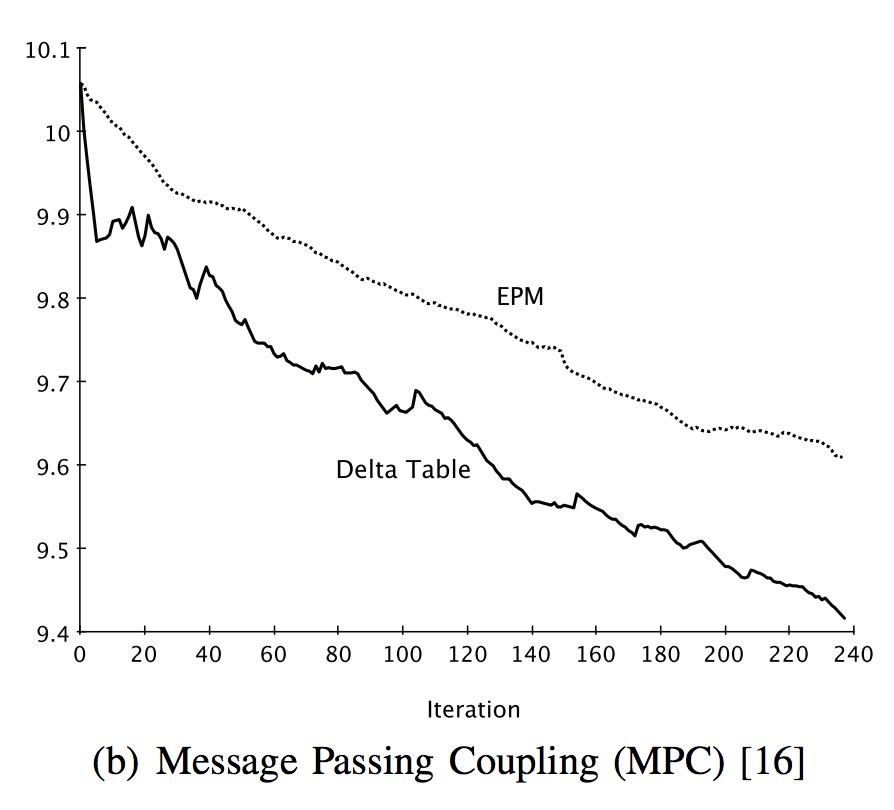
    Maintainability metric for Columba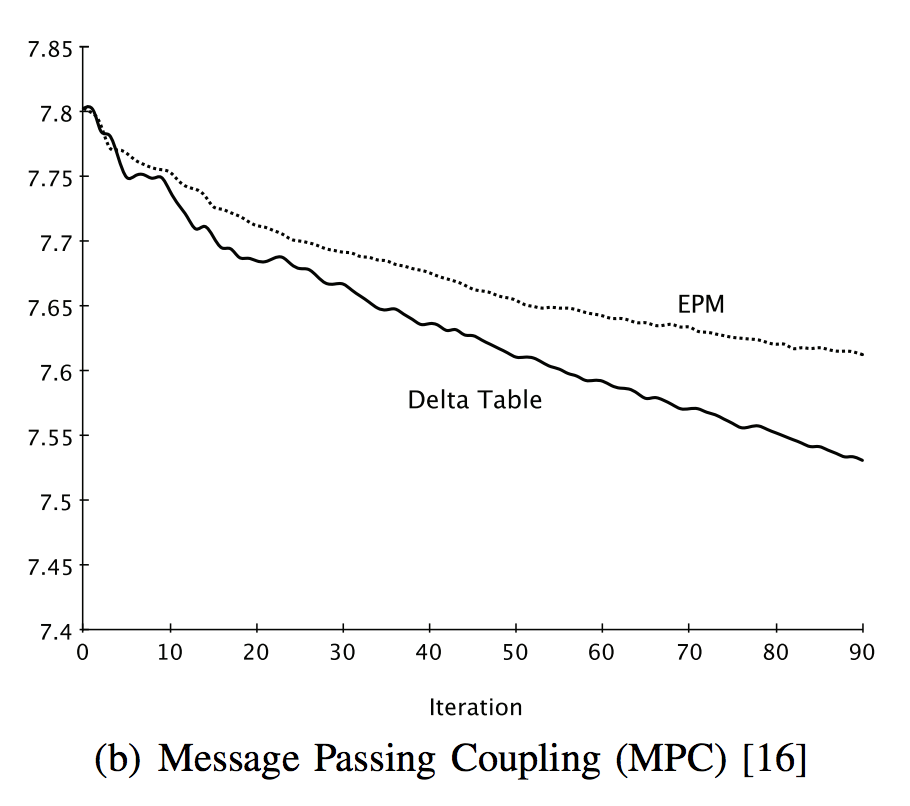 Columba The maintainability metric of MPC for the refactored design at each iteration is presented. In the approach using the Delta Table for both jEdit and Columba, the MPC decreases faster than the approach using the EPM. The MPC is a coupling metric, and the lower MPC represents the more improved maintainable software.

Conclusion

I propose a matrix computation-based refactoring candidate assessment metric. The metric in the Delta Table is the approximate measure, but it is sufficient to preliminarily assess the effects of the application of refactoring candidates in an extremely short time. This fast assessment can help the efficient refactoring candidate identification for the large-scale software.

Papers

Awards

  • Nov. 2013 - Oct. 2014, sole Principal Investigator, Post-Doctoral Fellowship Grant
    National Research Foundation of Korea (NRF), $33,000 [certificate] [translated version]